Introduction
Every year, a selection committee assigns seeds to college basketball teams across the country that determine their schedule to reach the National Championship (NCAA). The best teams in the country generally receive the top seeds (1-2) while lower-performing, less well-known teams, generally receive the lowest seeds (15-16). The seed is essentially a prediction of how far a team will progress in the tournament (Singh). The 1 seed is predicted to go to the final four, 4 seeds to make the Sweet Sixteen, and 16 seeds to be eliminated in the first round. However, March Madness is special because of its upsets. For this reason, we are interested in how seeds perform relative to expectations. What seeds tend to overperform while others underperform? Our research question is thus: “How have college basketball seeds performed in March Madness relative to their expected outcomes between 1985 and 2019?”
We were motivated to research this topic not only because we are devoted basketball fans (known affectionately at Duke as “Cameron Crazies”), but also because we found this research on this topic to be shockingly lacking. Most of the existing research is about trying to predict the results of March Madness to create a “perfect” bracket. For example, an article from the University of Nebraska Omaha is titled “Attempting to Predict the Unpredictable: March Madness” or “NCAA: Bold Predictions for March Madness 2019” (Kanzmeier, Odjakijan). By contrast, our research differs from traditional prediction models because rather than trying to predict the outcomes of the tournament, we want to determine which seeds generally outperform expectations. This also means that the scope of our project is larger because our data will analyze every tournament since the field expanded, rather than only observing one or a few tournaments.
We hypothesize that because of upsets, higher-ranked seeds on average underperform, while the lowest seeds tend to slightly overperform because of occasional upsets. We further hypothesize that 4 seeds will most frequently overperform relative to expectations because they are predicted to be eliminated in the Sweet 16, despite generally only having a few more losses than the top seeds. To be clear, we selected 1985 as the starting point because that was the year that the NCAA expanded to a 64-team tournament with 16 seeds. Still, we anticipate that we will begin to see more upsets after 2001 and 2011 when the NCAA expanded to 65 and 68 respectively. Since “play-in” games help to filter in more experienced seeds, they will likely perform better.
We do not believe there are any ethical issues regarding how the data were collected. The most common ethical concern when researching college sports is whether the data contains information that could harm the athletes. Many athletes experience abuse and hateful language from gamblers and fans on Twitter (Sanderson, Truax). This can lead to serious mental health concerns that endanger collegiate athletes some of whom are not even adults. However, this data only mentions program performance and omits the names of any players who might have performed poorly and thus be subsequently blamed by fans. For this reason, we do not see any ethical dilemmas with the data.
The source of our data is https://data.world/sports/ncaa-mens-march-madness, an online database for various datasets. The original data curator is Sport Reference which is essentially the standard for sports data sets and remains highly trusted. It contains box scores from most major sports, especially college basketball and NCAA tournaments. The data was originally collected by Kevin Johnson and Dave Quinn but has been continuously updated through different official sports data agencies. They founded it in 2004 when they began to collect data on college basketball and this data was collected through 2019. The data includes 2,205 different NCAA games ranging from 1985 to 2019, with 10 columns: the year of the game, the round of the game, the region name, the seed of the winning team and of the losing team, the score of the winning team and the losing team, the name of the losing team and of the winning team, and how many periods of overtime occurred (NA if the game ended in regulation time). This breaks down into 7 quantitative variables: the year of the game, the round of the game, the seed of the winning team and of the losing team, the score of the winning team and the losing team, how many periods of overtime occurred (NA if the game ended in regulation time), and 3 categorical ones: the region name and the name of the winning team and of the losing team.
We cleaned our data by checking to make sure that all relevant data was available from 1985-2019 and that there was no duplicate information. A check on duplicate entries helped to maintain the integrity of our analysis. Duplicate records for the same game or team in a given year could have skewed our results. We verified that the categorical variables, such as the region name and the names of winning and losing teams, did not contain anomalies or errors. For instance, we onfirmed that team names are spelled correctly and consistently across the dataset. We checked the numerical variables, such as the scores of winning and losing teams, to ensure they fell within reasonable ranges for basketball scores. Any outliers or unrealistic would have been investigated and addressed. The Big_Dance_csv dataset was cleaned into our march_madness dataset by only using the columns: year of the tournament, name of the team, the team’s seed, and their ranking at the end of the tournament.
Literature Review
In this article from the Journal of Sports Research, four statisticians from North Dakota State University attempted to predict the results of the 2015 and 2016 NCAA March Madness Tournaments using three different statistical models. The three methods that they used included a Bayesian logistic linear model with probability self-consistency, a machine learning method: a support vector machine, and a random forest method. Through each of these models, they quantified the success of the models by how many “points” they could earn in the bracket challenge. Essentially, points are generally determined using a double-point method. For example, if the model predicts a Round of 64 game correctly, it earns 1 point, the Round of 32 is 4 points, all the way to predicting the champion is worth 32 points. The total amount of points that can earned with a perfect bracket is 192. The models were broken down by what percentage of the points they won per round. For example, if they predicted three-fourths of the games in the first round, they would earn 75% of the points. They totaled these percentages to see which models did the best job at predicting the tournament overall. The data that they used to develop how the models would predict the 2015-2016 tournaments came from the 2007-2014 tournaments. The variables essentially included the relevant statistics for predicting a team’s performance like defensive rebounds per game and field goals per game.
For the 2015 tournament, the machine learning model performed the best with 60.4% of the points earned. The random forest model came in second with 57.3% of the points earned, and the Bayes model came in last with 43.2% of the points. For the 2016 tournament, the Bayes model got 52.08% the points while the random forest earned 51.6% and machine learning earned 49.5%. However, they noted that 2016 was interesting because UNC lost the championship even though they were about to win with .5 second left. Overall, they concluded that the machine learning and random forest models performed best, but that it is extremely difficult to predict using double point systems because the rounds build off each other.
Both our research and their research are interested in the outcomes of March Madness, but the connection goes deeper than that. Fundamentally, we are both trying to measure performance. However, they are trying to measure performance by finding what models can earn the most points for people who want to fill out March Madness brackets. By contrast, our research shows which March Madness seeds before best (in terms of surpassing or underwhelming expectations). Our research would provide a Bracketologist with context for making their choices. For example, they might be less likely to pick all 1 seeds in their Final Four because our research would show them that on average 1 seeds do not necessarily meet that expectation. On the other, their research would show a Bracketologist or even committee member working for the NCAA tournament how the tournament could look. It is not informing predictions, rather it is making predictions.
We found that this is part of a larger pattern in March Madness research. The vast majority of research is dedicated to predicting the outcomes of a tournament using basketball metrics like offensive rebounds per game. At its core, their research predicts the outcomes of the 2015-2016 tournaments. Our scope is thus much larger than theirs because we are analyzing tournaments from 1985-2019. We are not trying to predict the results of any given tournament. Rather, we are simply analyzing seed performance over that stretch. How do seeds perform relative to expectations? By answering that question, we are building on this research because we are not trying to simply make predictions for one tournament. We want to identify trends and average performance across all tournaments.
Methodology
Data Source and Collection
The data for this research project was obtained from the “march_madness.csv” file. The dataset contains information on college basketball teams participating in the NCAA March Madness tournament from 1985 to 2019. It encompasses a comprehensive record of every tournament team, from every year between 1985 and 2019, the teams seeds, their ranking at the end of the tournament. Ranking was determined by the number of wins each team won in the tournament and tiebreakers in this context were determined by the number of wins and seed that their opponent who defeated them had. Hence, a team who lost to the 1-seed in the first game would have a higher ranking than a team who lost to the 16-seed. We added a fifth variable to this dataset named “Differential” to quantify how each team performed relative to their seed. The Differential variable was determined by taking the teams Seed-(teams Ranking/4), since ranking is out of 64 (all teams in the tournament) and seed is out of 16 (by conference).
We address our research question by analyzing the performances for each seed. This was done by analyzing the differential values by seed to visually represent the distribution of outcomes for different seeds. We created a scatterplot measuring the effect of seed by ranking by year. We also measured the effect of year on differential by seed. This enabled us to identify any outliers or patterns in the data.
Statistical Tools Used
To provide a well-rounded analysis of our dataset, we used a variety of statistical tools to explore our question. We started with simple table analysis, looking for outliers through filtering and sorting to find examples of teams strongly betraying their initial seed, either jumping up or down sharply in ranking. Then, we created scatter plots to start finding patterns within the data, either between ranking and seed, or differential and seed. As we noticed relationships appearing in our plots, we decided to move on to a more numerical analysis of these patterns through regression models. Linear models proved to be the most appropriate in our situation, since we were attempting to model the relationship between quantitative variables, which ranged from 1 to 16 for Seed, 1 to 64 for Ranking, and -15 to 15.75 for Differential. Since we were only working with two variables in the cases we examined, we did not need to worry about choosing between additive and interactive models. Finally, we also used some more simple statistical methods such as mean to demonstrate more specific cases (such as how seed changes mean differential).
Code and Analysis
Data Exploration
| 2018 |
Virginia |
1 |
56 |
-13.00 |
| 2002 |
Cincinnati |
1 |
32 |
-7.00 |
| 2017 |
Villanova |
1 |
32 |
-7.00 |
| 2015 |
Villanova |
1 |
31 |
-6.75 |
| 2004 |
Kentucky |
1 |
30 |
-6.50 |
| 1985 |
Villanova |
8 |
1 |
7.75 |
| 2014 |
Connecticut |
7 |
1 |
6.75 |
| 1988 |
Kansas |
6 |
1 |
5.75 |
| 1997 |
Arizona |
4 |
1 |
3.75 |
| 1989 |
Michigan |
3 |
1 |
2.75 |
The differential variable allows us to explore the extreme cases of how seeds can perform relative to their predictive outcome. For instance, South Carolina in 1997 and Duke in 2012 were among the worst performers compared to their seeds, falling from 2 seeds to rank 63 and 61 respectively. On the other hand, the lowest seeds to win the championship include 1985 Villanova and 2014 Connecticut, 8 and 7 seeds respectively.
Exploratory Data Analysis
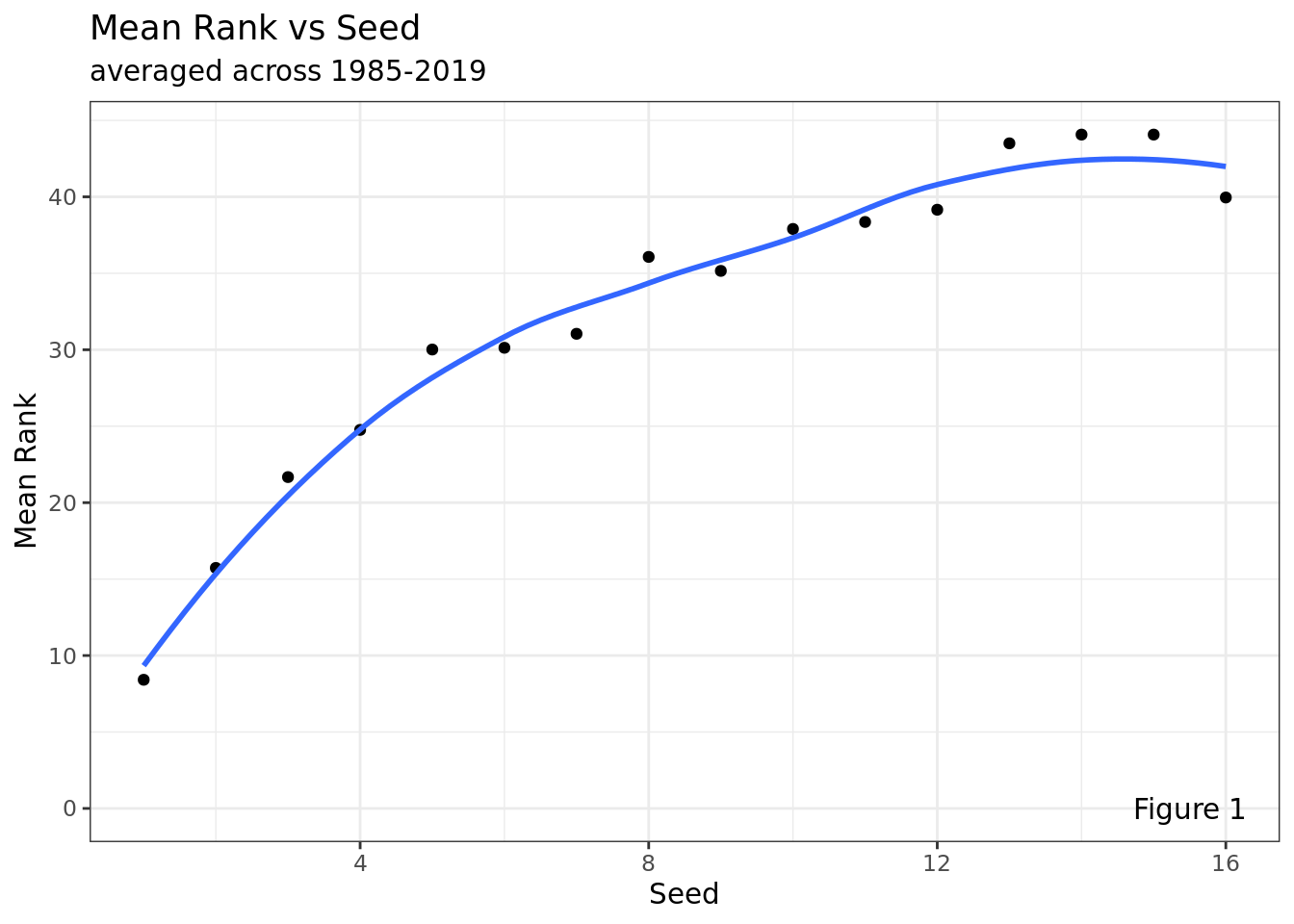
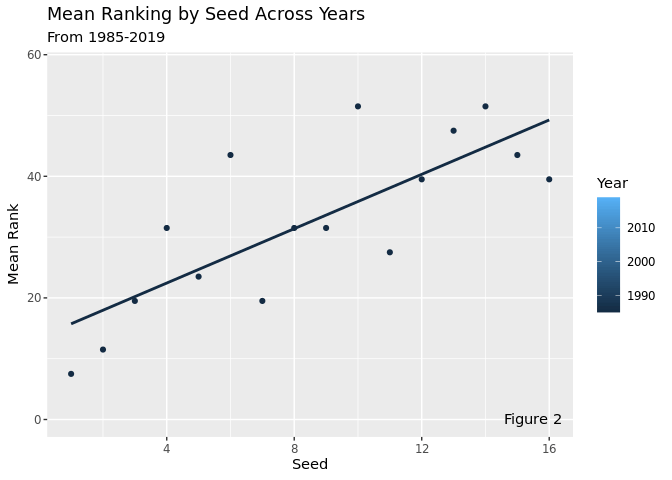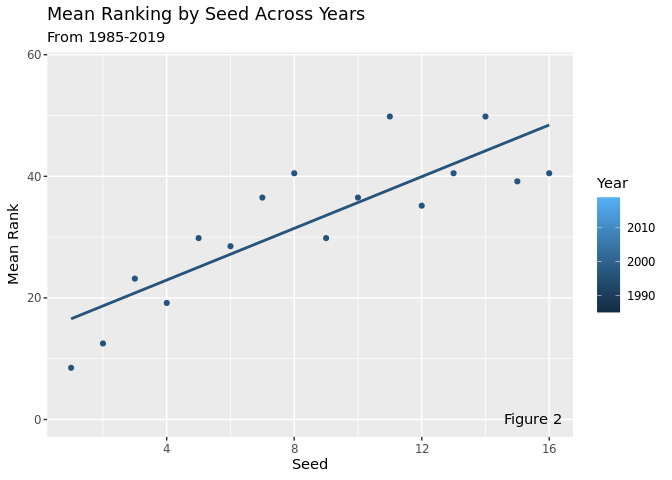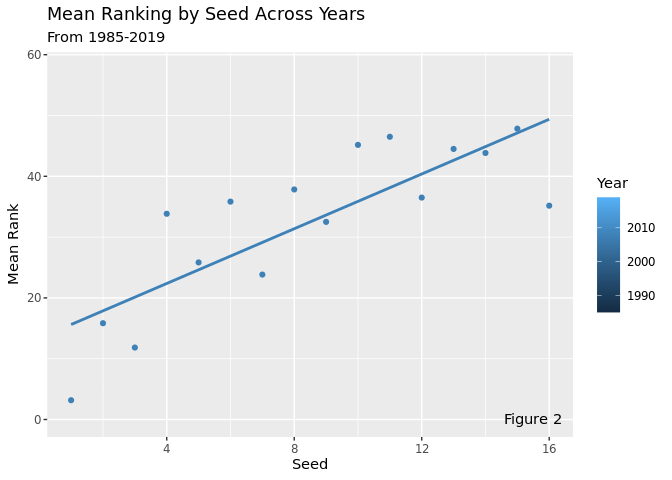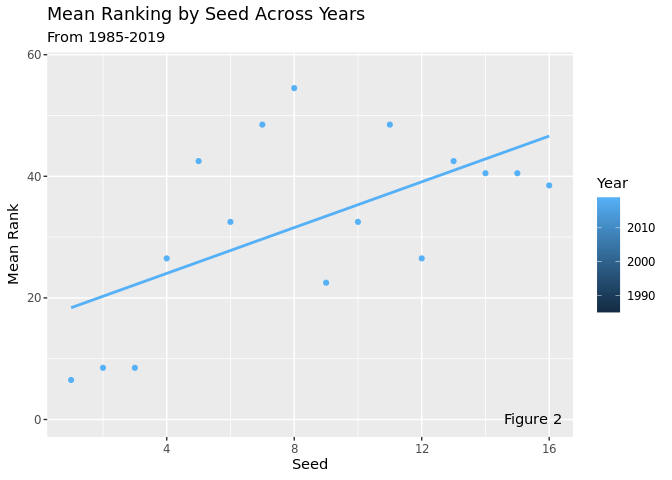
We can see from this graph that there is a strong, positive relationship between a team’s rank and their seed. Lower seeds have a better chance of over performing, and so have a higher rank on average. Conversely, it is harder for a 1, 2, or 3 seed to have a high rank. It is important to note that the 8 seed, for example, has a similar mean rank to the 16 seed. This represents the balance between being a better team (high seed) and having a low bar to outperform (low seed).
`geom_smooth()` using formula = 'y ~ x'
`geom_smooth()` using formula = 'y ~ x'
This plot takes the average ranking of the 4 seeds each year and animates them over time. This visualization shows how the relationship between seed and rank remains relatively constant across all years, although there is a high amount of variability year-to-year. There is an especially high amount of variability with the middle seeds, while the high seeds and the low seeds tend to stay more constant. The relationship between seed and mean rank remains positive and relatively strong across all years, which means that top seeds are more likely to perform well than low seeds, which makes sense, since seeds are supposed to represent expected success in the tournament.
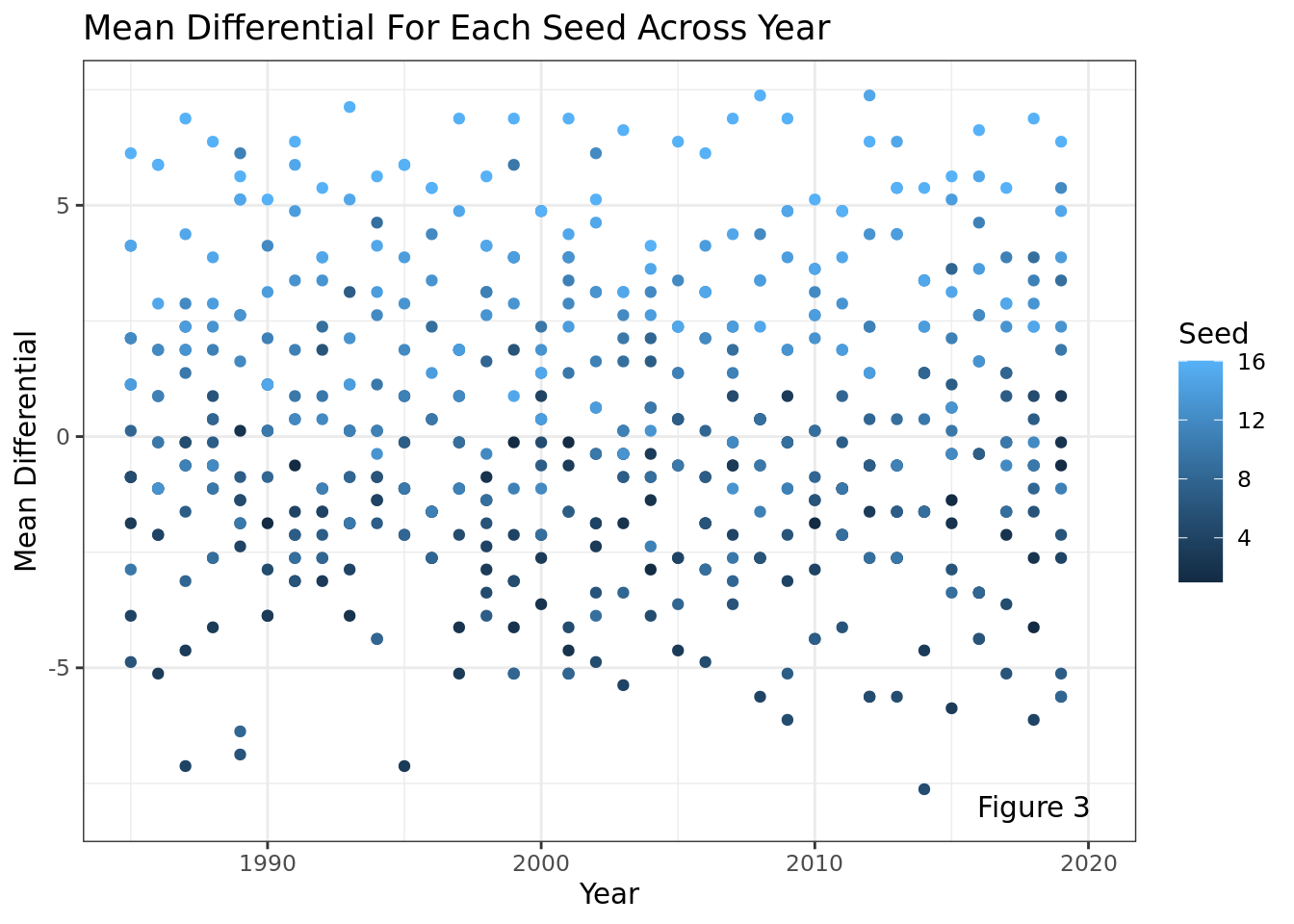
As stated prior, the differential variable enables us to understand the extremes how seeds can overperform or underperform relative to their predictive outcome. Looking at this visualization, it is clear that lower seeds on average had a much higher differential across the years (5-10), with the large majority of data points in the 0-10 region being from seeds 12-16. On the other hand, higher seeds (1-4) on average had a significantly lower differential in the -10 to -15 range, demonstrating that higher seeds on average do worse than lower seeds.
Further Analysis
| 16 |
6.0107143 |
| 15 |
3.9821429 |
| 14 |
2.9821429 |
| 12 |
2.2107143 |
| 13 |
2.1250000 |
| 11 |
1.4107143 |
| 10 |
0.5250000 |
| 9 |
0.2107143 |
| 7 |
-0.7607143 |
| 8 |
-1.0178571 |
| 1 |
-1.1035714 |
| 6 |
-1.5321429 |
| 2 |
-1.9321429 |
| 4 |
-2.1892857 |
| 3 |
-2.4178571 |
| 5 |
-2.5035714 |
Looking at average differential by seed, 5 and 4 seeds actually rank among the worst overall performers within the dataset (having the 1st and 3rd worst average differentials with -2.5 and -2.19 respectively). On the other side of the spectrum, low seeds always have the highest differentials, with the 16-seed leading the way with an average rank increase of 6.01, which makes sense since they have less to lose.
Modeling
We decided to create 2 different models based off of our exploratory data analysis. One to model the relationship between ranking and seed, and one to model the relationship between differential and seed. Since year did not seem to be a factor in either of these relationships, we decided to exclude it and go with simple linear models with only one variable. We are interested in learning exactly how a team’s seed effects their performance in the tournament, both in terms of ranking and seed.
Results
Model
| (Intercept) |
15.231429 |
0.7060284 |
21.57339 |
0 |
| Seed |
2.031597 |
0.0730157 |
27.82410 |
0 |
\[
\widehat{Ranking} = 12.23 + Seed \times 2.03
\]
This linear model describing ranking in function of seed reflects the notion that higher seeds (e.g. 1 and 2 seeds) perform better than lower seeds (e.g. 15 and 16 seeds), which makes sense by the definition of a seed. The intercept goes out of the scope of our data since it describes a 0-seed, but the linear model shows that 1-seeds will generally be ranked 14.26 / 64, and that this value will go up by 2.03 every time Seed goes up by 1.
| (Intercept) |
-3.8078571 |
0.1765071 |
-21.57339 |
0 |
| Seed |
0.4921008 |
0.0182539 |
26.95862 |
0 |
\[
\widehat{Differential} = -3.8 + Seed \times 0.5
\] The model describing differential provides a more interesting insight: higher seeds actually tend to underperform, while lower seeds are more likely to overperform. The model shows that 1-seeds generally drop 3.3 ranks, but that as seed increases, differential goes up by 0.5, indicating that upsets are actually more common than not!
Conclusion
As described prior, our core research question was, “How have college basketball seeds performed in March Madness relative to their expected outcomes between 1985 and 2019?”
First, context for this question can be gleaned by looking at the differential variable across many years and seeing which teams have maximally underperformed or overperformed compared to their expected outcome (seed). South Carolina in 1997 and Duke in 2012 are two striking examples that demonstrate the power of the differential variable in illustrating these contrasts, which is key to the rest of our argument.
The “plot-data” visualization further illustrates trends in the differential variable, specifically showing that low seeds are historically much more likely to have a higher differential than high seeds. This provides further credence to our argument that on average, higher seeds do worse than lower seeds in March Madness. Furthermore, the differential linear regression shows 1-seeds tend to underperform by ~3.3 ranks, and as seed increases from there, rank increases by ~0.5, showing that the lower seed a team is, the more likely they are to overperform. This has been a fairly constant trend over the last 3-4 decades, as shown by the animated graph.
On the other hand, the linear model using ranking seems to refute some our previous hypotheses, as it shows that every time you increase seed by 1, their ranking increases on average by 2.03, suggesting that higher seeds are more likely to overperform. Further nuance is seen in the average differential by seed table, which shows that 4 and 5 seeds are actually the overall worst performers, as compared to either of the extremes. This shows that our original hypothesis (that 4 seeds tended to be the best performers) has not been the case over the past decades.
Scope of Inference: Since this was an observational study, we did not attempt to show a cause-effect relationship, nor can these results prove definitively how any given tournament will result. For example, although 4 seeds tended to be among the worst performers, a 4-seed actually won the most recent March Madness tournament (UConn in 2023). Thus NCAA selection committees should not use these findings to attempt to change any traditional methods of seeding (rather than should continue to analyze resumes). Thus, while our results do show how seeds performed relative to expectations on average over the course of decades, this cannot show a cause-effect relationship between any given seeding and performance.
Discussion
In summary, we have learned that there is a tremendous amount of nuance in our research question - while differential data illustrate that low seeds are historically much more likely to overperform compared to higher seeds, a trend that has stayed relatively constant over the last few decades, linear modeling by ranking suggested the opposite, indicating that higher ranked seeds were more likely to perform better. Specifically, the differential linear regression showed that 1-seeds tended to underperform on average by ~3.3 seeds, increasing by 0.5 each additional seed. On the other hand, linear modeling by ranking showed that ranking on average increased by 2.03 per higher seed, proving the opposite trend. Interestingly, the average differential by seed table indicated that the 4 and 5 seeds have actually been the worst performers historically, straying away from the two extremes suggested prior. As shown, our research question is quite multifaceted, with many variables and dynamics at play.
The first major limitation of our analysis is that our core examination of differentials isn’t particularly strong due to the lack of conclusivity in the variable. Firstly, by the very nature of being a higher seed, it is much more unlikely to overperform since there are less seeds above you. For example, it’s impossible for a 1 seed to overperform and a 2 seed can only overperform by winning the championship, while a 16 seed could overperform significantly by winning just one game. Furthermore, while ranking by seed aims to normalize by difficult of opponents, the differential variable doesn’t, which makes it hard to standardize comparisons between different seeds. Thus, to improve this, creating a new variable which standardizes for all of these biases in the current differential variable would enable a much more sound analysis.
Secondly, our system of team ranking, which was based on number of tournament wins but broke ties based on the seed of the opponent a team lost to, is flawed. Specifically, this method of tiebreaking isn’t great because it doesn’t speak to a team’s specific capabilities, but rather ranks them based on external games within a given March Madness tournament, which confounds the data. To improve this, one could use a more statistically based classification, such as that used by kenpom.com, to numerically establish the ranking.
Finally, the dataset isn’t fully representative of all of March Madness, as it only portrays trends between 1985 and 2019, excluding all of the pre-tournament of 64 and the last 4 years as well. This means that a significant amount of data extending from 1939 to 1984 and after 2019 is not included. While the former obviously wouldn’t be the best data, it still represents a considerable portion of the tournament’s history and prevents us from analyzing the full evolution of trends in ranking changes. Additionally, as mentioned in the scope of inference, this is purely an observational study, meaning that only correlations can be derived as opposed to causation. To improve this, we can continue collecting data and perhaps look into the pre-tournament of 64 data, carry out similar modeling analyses, and see if the same trends are reflected as are in our data. Unfortunately, it will never be possible to establish causation (unless anyone’s interested in game fixing!).
There aren’t any issues pertaining to our data’s reliability and validity, as it is an official, well-sourced, and thorough dataset. The major problems with our statistical analysis have to do with the variables used, as opposed to the regressions and visualizations employed. Using more representative and less confounded variables will ensure better data and more precise trends.
In addition to the potential improvements suggested above, ideas for future work include extending this analysis to the NBA in-season tournament, women’s March Madness, or to other sport tournaments with a similar bracket structure, such as college football. Additional avenues for discussion include taking a more statistical approach by looking at advanced statistics or exploring what factors are actually responsible for teams overperforming/winning.