Multiple regression I - SUGGESTED ANSWERS

STA 199

How to write an indicator function:

\[ level = \begin{cases} 1 & \text{if condition is met}\\ 0 & \text{otherwise} \end{cases} \]

Today

By the end of today you will…

• understand the geometric picture of multiple linear regression
• be able to build, fit and interpret linear models with \(>1\) predictor

Load packages and data

library(tidyverse)
library(tidymodels)
library(scatterplot3d)
library(palmerpenguins)

Today’s data is a collection of tech stock prices from January 1st 2020 to December 31st 2021. I pulled this data off Yahoo finance using their API via the tidyquant package July 2022.

stocks = read_csv("https://sta101-fa22.netlify.app/static/appex/data/stocks2.csv")

\(R^2\) and checking model fit

Review + Reference

\(R^2\), aka “the coefficient of determination” is a way to see how well a given model fits the data. Formally,

\[ R^2 = 1 - \frac{\sum_i resid_i^2}{\sum_i (y_i - \bar{y})^2} \]

where \(\bar{y}\) is the mean of all y values.

In words,

\[ R^2 = 1 - \frac{\text{sum of squared residuals}}{\text{sum of outcome squared distance from the mean}} \]

Let’s focus on the word version to build intuition.

• The sum of squared residuals is a measure of how wrong our model is (how much our model doesn’t explain)

• The denominator is proportional to the average square distance from the mean, i.e. the variance, i.e. the amount of variability in the response y.

• Together, the fraction represents the proportion of variability that is not explained by the model.

If the sum of squared residuals is 0, then the model explains all variability and \(R^2 = 1 - 0 = 1\).

Similarly if the sum of squared residuals is the same as all the variability in the data, then model does not explain any variability and \(R^2 = 1 - 1 = 0\).

Final take-away: \(R^2\) is a measure of the proportion of variability the model explains. An \(R^2\) of 0 is a poor fit and \(R^2\) of 1 is a perfect fit.

How to find \(R^2\)

To find \(R^2\) simply call the function glance() on your modelFit, e.g.

modelFit = linear_reg() %>%
  set_engine("lm") %>%
  fit(outcome ~ predictor, data = data_set)
  
glance(modelFit)$r.squared

Two predictor main effects model and notation

\[ y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \epsilon \]

• \(y\): the outcome variable. Also called the “response” or “dependent variable”. In prediction problems, this is what we are interested in predicting.

• \(x_i\): the \(i^{th}\) predictor. Also commonly referred to as “regressor”, “independent variable”, “covariate”, “feature”.

• \(\beta_i\): “constants” or coefficients i.e. fixed numbers. These are population parameters. \(\beta_0\) has another special name, “the intercept”.

• \(\epsilon\): the error. This quantity represents observational error, i.e. the difference between our observation and the true population-level expected value: \(\beta_0 + \beta_1 x\).

Effectively this model says our data \(y\) is linearly related to the \(x_1\) and \(x_2\) but is not perfectly observed due to some error.

An example

Let’s examine the first quarter of 2020 high prices of Microsoft, IBM and Apple stocks to illustrate some ideas.

MSFT - Microsoft Corp - x1 IBM - IBM Corp - x2 APPL - Apple Corp - y

stocks_subset = stocks %>%
  slice(1:62)

scatterplot3d(stocks_subset[,c("MSFT.High",
                          "IBM.High",
                          "AAPL.High")],
              pch = 19, 
              color="steelblue",
              xlab = "MSFT High $", ylab = "IBM High $", zlab = "AAPL High $") 

Warning: Unknown or uninitialised column: `color`.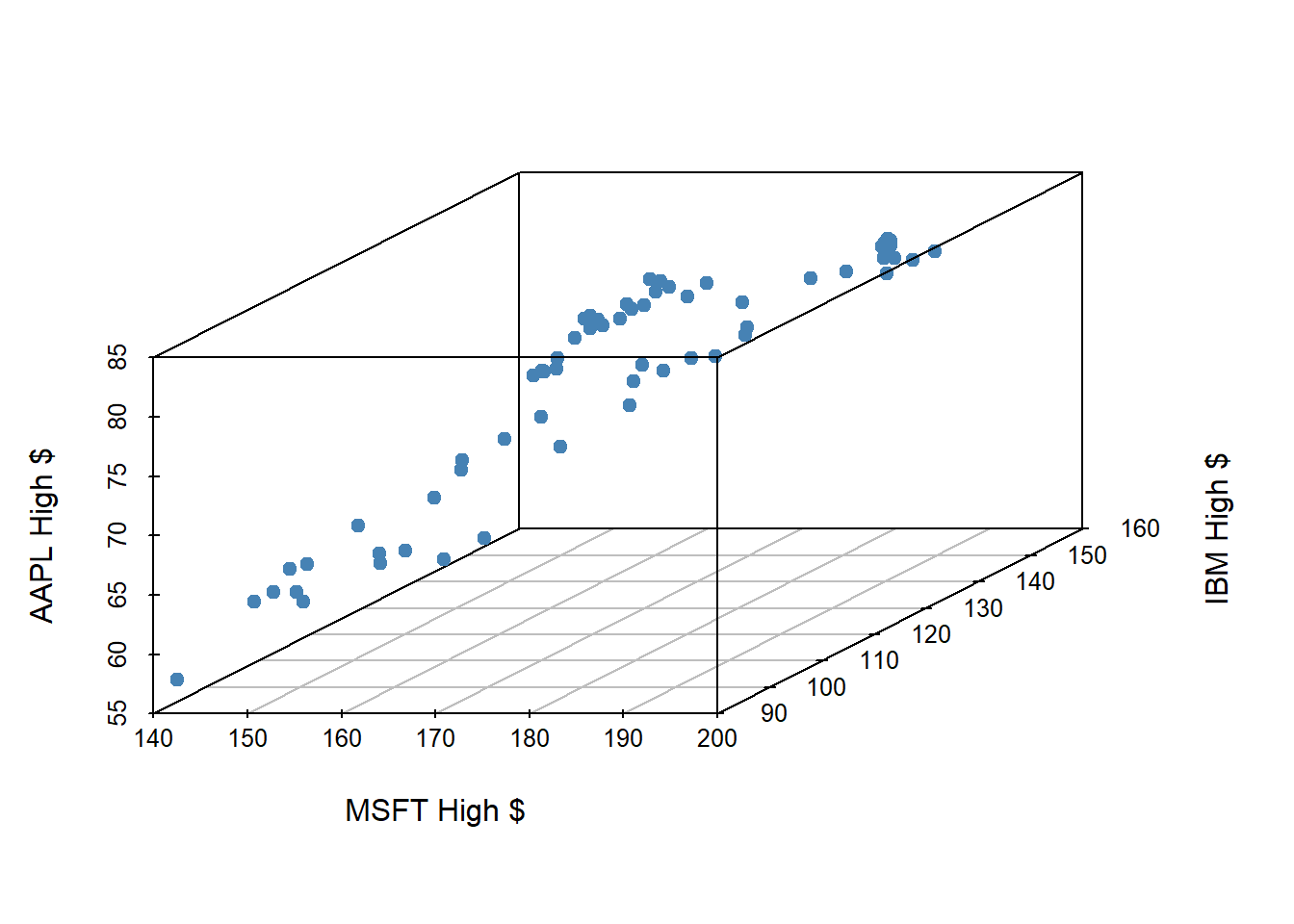

• If we have three measurements (variables) then each observation is a point in three-dimensional space. In this example, we will investigate Apple stock price’s relationship with the other variables in the model, using MSFT and IBM price as predictors.

• In general, the total number of measurements, i.e. variables (columns) in our linear model represents the spatial dimension of our model.

• Our fitted linear model no longer looks like a line, but instead looks like a plane.

plot3stocks = scatterplot3d(stocks_subset[,c("MSFT.High",
                          "IBM.High",
                          "AAPL.High")],
              pch = 19, 
              color="steelblue",
              xlab = "MSFT High $", ylab = "IBM High $", zlab = "AAPL High $") 

Warning: Unknown or uninitialised column: `color`.

model  = lm(AAPL.High ~ MSFT.High + IBM.High, data = stocks_subset)
plot3stocks$plane3d(model, col = "darkred")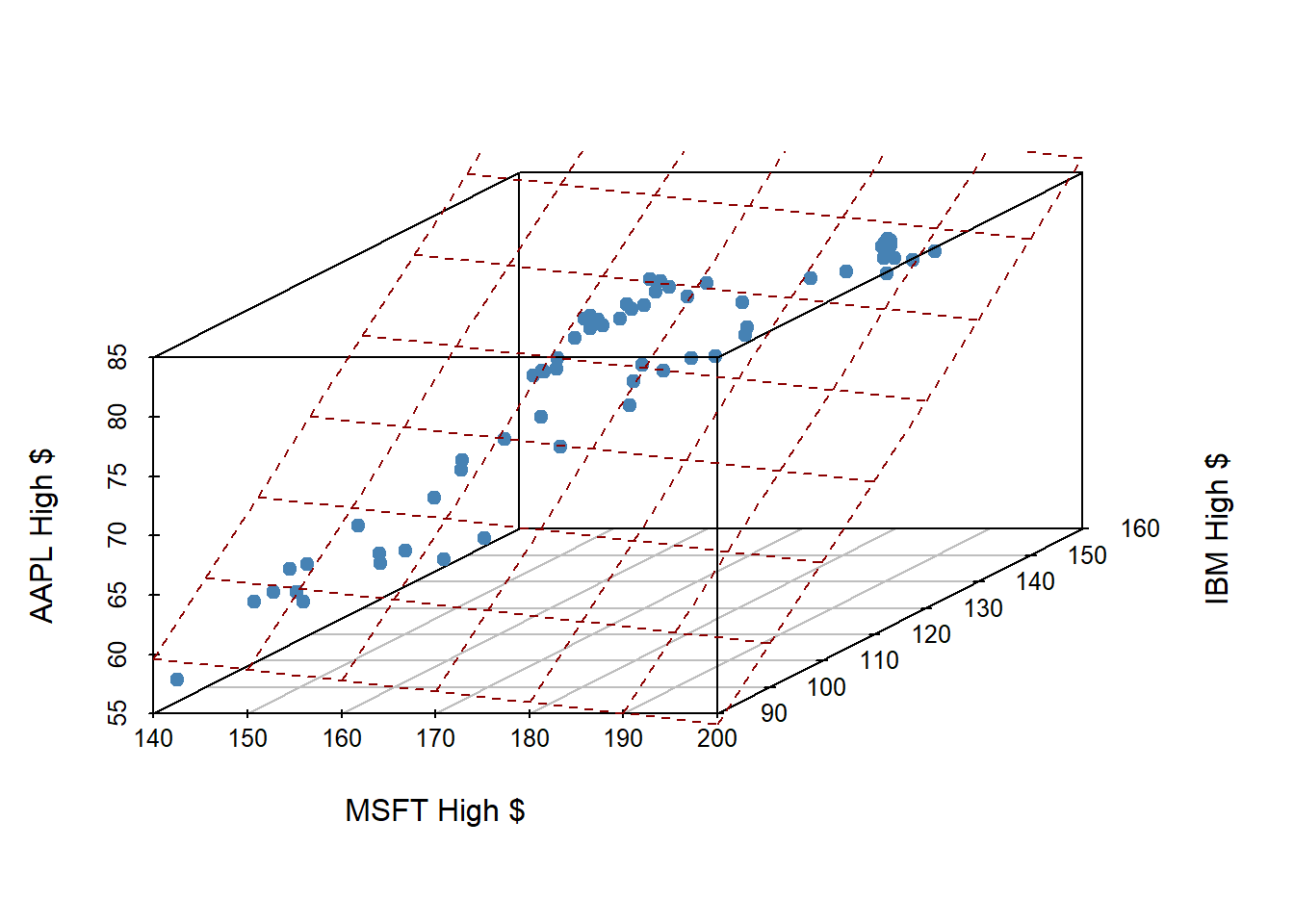

• This plane shows our prediction of AAPL price (\(y\)) given both MSFT price (\(x_1\)) and IBM price (\(x_2\))

Fitting an additive multiple regression model in R

Example:

myModelFit = linear_reg() %>%
  set_engine("lm") %>%
  fit(outcome ~ predictor1 + predictor2 + predictor3 + ..., data = data-set-here)

You can subsequently print the coefficients (\(\beta\)s) to the screen by simply typing the model name, e.g. myModelFit or calling the tidy() function on your fitted model, e.g. tidy(myModelFit).

Fit your model

In the code chunk below, fit the additive multiple regression model described above where

\(y\): AAPL high price, (APPL.High) \(x_1\): MSFT high price, (MSFT.High) \(x_2\): IBM high price. (IBM.High)

Then write the equation of your fitted model below.

• Note: you should change the name of “myModelFit” to be something more meaningful, e.g. apple_high_fit

apple_high_fit <- linear_reg() |>
  set_engine("lm") |>
  fit(AAPL.High ~ MSFT.High + IBM.High, data = stocks)

tidy(apple_high_fit)

# A tibble: 3 × 5
  term        estimate std.error statistic   p.value
  <chr>          <dbl>     <dbl>     <dbl>     <dbl>
1 (Intercept)    4.25     5.85       0.726 4.68e-  1
2 MSFT.High      0.542    0.0100    54.0   9.82e-211
3 IBM.High      -0.105    0.0498    -2.11  3.53e-  2

The equation of the plane above:

$$

= 4.25 + 0.542MSFT - 0.105IBM

$$

interpret

Interpret the coefficient associated with MSFT high price in your equation above.

Holding IBM constant, for a 1 $ increase in msft, we estimate on average a .542 $ increase in apple

IBM

Holding msft constant, for a 1 $ increase in IBM, we estimate on average a 0.105 $ decrease in apple

r-squared

What is the R-squared of this model? Calculate and interpret it below

glance(apple_high_fit)$r.squared

[1] 0.8663961

The amount of variability in our response apple stock that is explained by our model with msft and ibm is roughly 86.6%.

Penguins: Last Time

We explored the relationship between body mass and flipper length. We also explored the relationship between body mass and island. What if we want to include both coefficients?

Now, fit an additive model to assess the relationship between our response variable body mass, and our explanatory variables flipper length and island. Produce the summary output. Write out the estimate regression equation below. Note, change the text of the indicator function to match the situation.

peng_model <- linear_reg() |>
  set_engine("lm") |>
  fit(body_mass_g ~ flipper_length_mm + island , data = penguins) 

tidy(peng_model)

# A tibble: 4 × 5
  term              estimate std.error statistic  p.value
  <chr>                <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)        -4625.     392.      -11.8  4.29e-27
2 flipper_length_mm     44.5      1.87     23.9  1.65e-74
3 islandDream         -262.      55.0      -4.77 2.75e- 6
4 islandTorgersen     -185.      70.3      -2.63 8.84e- 3

$$

= -4625 + 44.5flipper - 262Dream - 185*Tor

\

Dream = \[\begin{cases} 1 & \text{if Dream level}\\ 0 & \text{else} \end{cases}\]

\

Tor = \[\begin{cases} 1 & \text{if Torgersen level}\\ 0 & \text{else} \end{cases}\]

$$

– Interpret the slope coefficient for flipper length in the context of the problem

Holding island constant, for a 1 mm increase in flipper length, we estimate on average a 44.5 g increase in body mass

– Interpret the slope coefficient for Dream island in the context of the problem

Holding flipper length constant, we estimate on average a 262 g decrease in body mass for penguins on the Dream island compared to Biscoe

– Predict the body mass of a penguin with a flipper length of 200 on the Dream island

predict(peng_model, data.frame(flipper_length_mm = 200, island = "Dream"))

# A tibble: 1 × 1
  .pred
  <dbl>
1 4021.

Visualize

Now, let’s visualize the data. First, let’s define our coefficients and use this information to plot this model.

b0 <- -4625 
bD <- -262
bT <- -185
b1 <- 44.5

penguins %>%
ggplot(aes(x = flipper_length_mm, y = body_mass_g, color = island)) +
  geom_point() +
  theme_bw() +
  geom_abline(intercept = b0, slope = b1, color = "#F8766D", lwd = 1) +
  geom_abline(intercept = b0 + bD, slope = b1, color = "#00BA38", lwd = 1) +
  geom_abline(intercept = b0 + bT, slope = b1, color = "#619CFF", lwd = 1) +
  labs(x = "Bill length (mm)",
       y = "Body mass (g)",
       title = "Additative Model between Length, Mass, and Island")

Warning: Removed 2 rows containing missing values (`geom_point()`).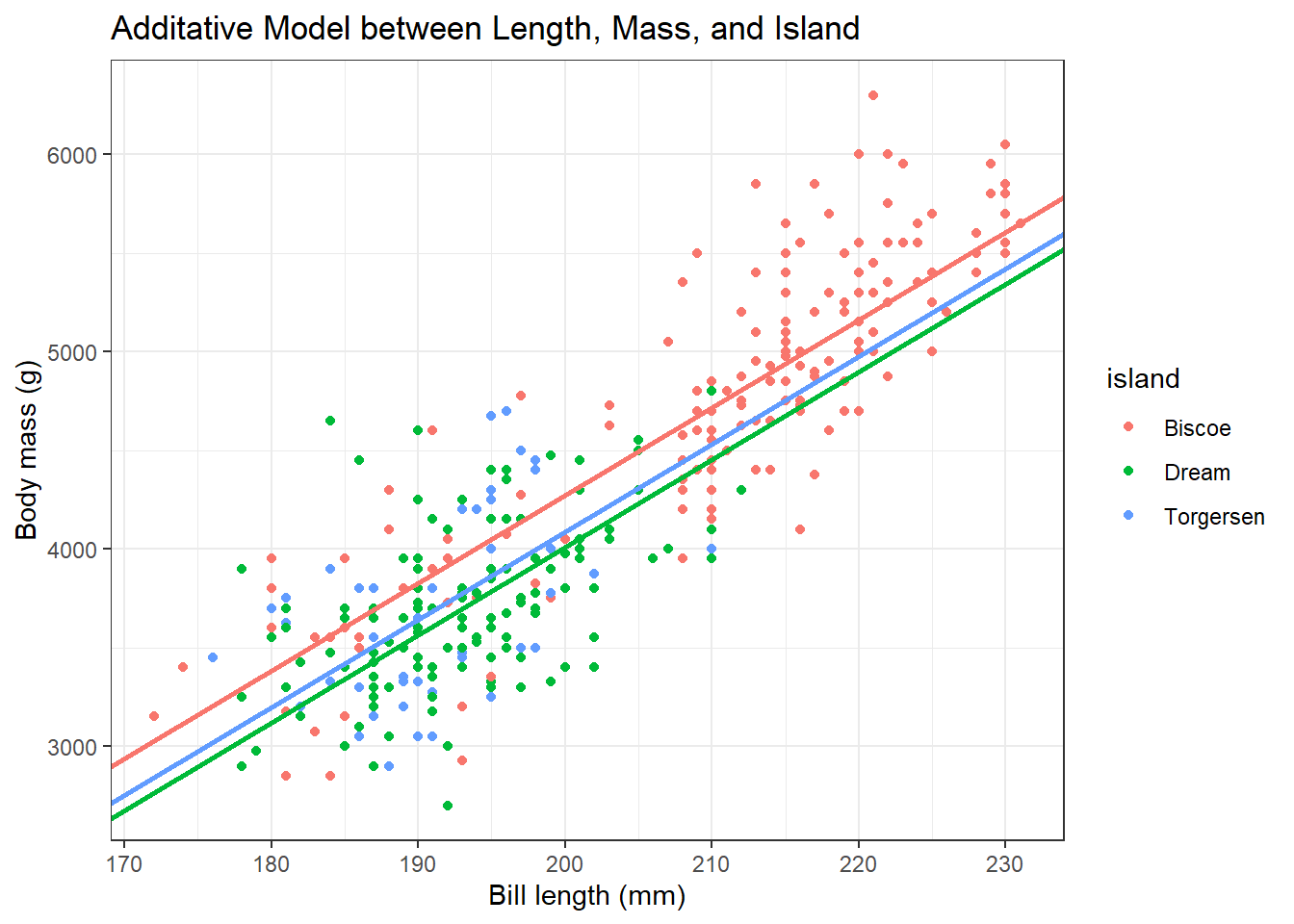

How does this differ from an interaction model?

Hint! Look at the slopes and compare to ae-15!