Hypothesis Testing

Lecture 21

Dr. Elijah Meyer

Duke University
STA 199 - Fall 2023

2023-11-09

Checklist

– Clone ae-21

– Keep up with Slack

– Draft Report Due November 15

– Exam-2 released November 16

— Cumulative with a focus on content post Exam-1

Project Feedback Expectations

– Close Issues on GitHub

– Incorporate feedback into Draft Report

Note: You do not need to go back and change your proposal

Warm up: Notation Check

– \(\mu\)

– \(\hat{p}\)

– \(\bar{x}\)

– \(\pi\)

Warm up: Notation Check

– \(\mu\) – True mean

– \(\hat{p}\) – sample proportion

– \(\bar{x}\) – sample mean

– \(\pi\) – True proportion

Warm up

Last time, we tested if you could read Martian. The null and alternative hypotheses were as followed:

\(Ho: \pi = 0.5\)

\(Ha: \pi > 0.5\)

– Why \(\pi\)?

– Why 0.5?

– Why > ?

Last Time

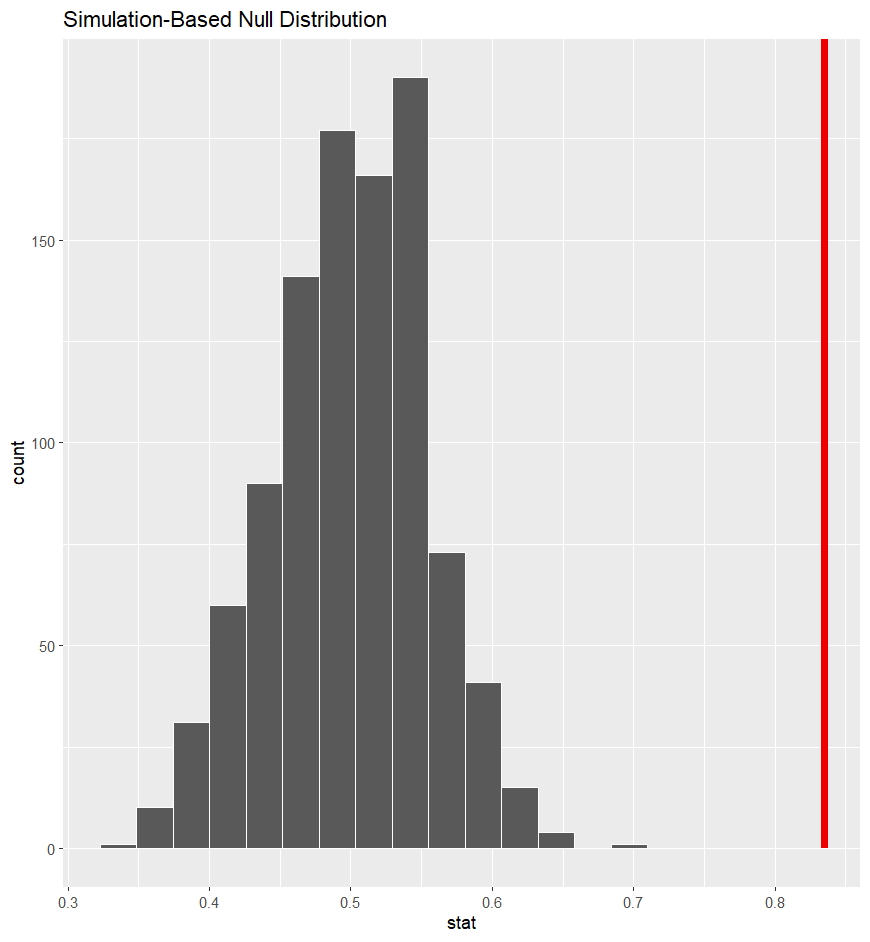
– Based on the visualization, is it likely to see our statistic under the assumption of the null hypothesis?

P-value

A statistical tool to help back up our visual conclusion is called a p-value. The definition of a p-value can be broken down into the following part:

– probability

– of observing our statistic

– or something “more extreme”

– given that the null hypothesis is true

Note: When we say more extreme, we either mean greater, smaller, or different. This is dictated by our alternative hypothesis!

P-value

– What is our p-value here?

• But probabilities can never be 0, so we report this as < 0.001.

How we use the p-value

We use p-values to write decisions and conclusions:

– Decision: Reject or Fail to reject the null hypothesis

– Conclusion: Strong or Weak evidence to conclude the alternative hypothesis

ae-21

— Why we can’t conclude the null

— hypothesis testing